The
NULL-DATA Cycle
To express the completeness of input criteria
for data, the circuits have to start out in an
all-NULL state. After each data set resolution
the circuit must be returned to an all NULL state
before the next data set is presented for resolution,
so the circuit must cycle alternately between
the all NULL state and the data resolution state.
Now we must determine when the circuit enters
the all NULL state from a data resolution state.
If we can determine when the circuit is in an
all NULL state, then we will know when it is ready
for a new set of input data to be resolved.
It can be seen from the truth tables of Figure
1 that the completeness of input criteria is not
enforced for NULL values in relation to data values.
If one input value is NULL then the result value
will become NULL. Referring to Figure 2, it is
possible for a single input value to become NULL
and drive all the result values to NULL. For instance
if D becomes NULL the NULL value will propagate
through gates 1, 3, 4, 6, 7, 8 and 9 driving all
of the result values to NULL while there are still
data values lingering on the input and internal
to the circuit.
The NULL Wave Front
The second step in making Boolean logic
symbolically complete is for the gates to enforce
the completeness of input criteria for NULL in
relation to data (as well as for data in relation
to NULL). This can be accomplished in two
ways:
| 1.
|
Another
(i.e., fourth) value can be added
to the primitive mutually exclusive value
assertion domain of the logic. |
| 2.
|
A
feedback variable can be added to each gate.
|
The Intermediate Value Solution
Adding another value to the primitive mutually
exclusive value assertion domain of the logic
provides a solution that is purely delay
insensitive and purely symbolically complete.
We will add another value called the Intermediate
value and configure the truth tables as shown
in Figure 3.
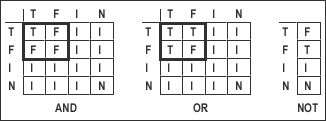
Figure
3. Intermediate value truth tables.
We now have a four value logic. It can
be seen from the truth tables that a gate will
only assert a data result value when both input
values are data, and will only assert a NULL result
value when both input values are NULL. The truth
tables directly enforce the completeness of input
criteria for both data and NULL. When the result
values are all NULL the inputs are all NULL and
circuit is completely reset and ready for a new
data set. When the result values are all data,
a complete data set is presented at the input
to the circuit and its resolution is completed.
The result values transition from all NULL through
Intermediate values to all data then from all
data through Intermediate values to all NULL.
The watcher of the result values looks for all
data and all NULL at the output and simply ignores
Intermediate values. |