The completeness of input criteria is the key to speed independent logic circuits. The completeness of input criteria for each gate scales up for combinational circuits as a whole. Consider Figure 2.

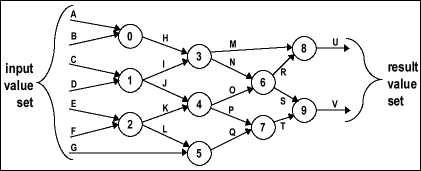
Figure 2. Example of a combinational circuit.

Assume that the circuit is in an all NULL state in that all of the input values, internal values and result values are all NULL. If one input value, A for instance changes to data, gate 0 will continue asserting a NULL value. Gate 0 does not assert a data value until both input values for A and B are data. To see how this behavior scales up for the whole circuit consider gate 6. Gate 6 will not assert a data value until both inputs N and O are data at the gate. It doesn't matter how long it took for the data values on N and O to propagate to the gate 6 input or in which order they arrive. When both input values are data at gate 6, it asserts the correct result data value. This transition from NULL to data also asserts the validity of that result data value and asserts the completion of gate's resolution entirely symbolically. No other aspect of expression and no time relationship is associated with the assertion of these three facts. Each gate is a synchronization node managing an orderly wave front of correct result values propagating through the circuit.

The circuit as a whole will not assert a complete set of result data values until there is a complete set of input data values and the resolution of the input data values has propagated through the circuit. If one input value remains NULL at least one result value will remain NULL. For instance, if all the input values are data except G, which remains NULL, then gate 5 will assert a NULL result value for Q, gate 7 will assert a NULL result value for T and gate 9 will assert a NULL result value for V. When G becomes data, the input data set is complete. The data value will propagate through the circuit and V will become data and the result data set will be complete (all datas, no nulls).

When all the result values become data, it means that a complete set of input data values are presented to the circuit, that the resolution of the presented input value set is complete and the asserted set of result values is the correct and valid resolution of the presented set of input data values. This is what is meant by the completeness of input behavior of each gate scaling up for a circuit as a whole. The circuit does not assert a complete set of result data values until a complete set of input data values are present at the input to the circuit and resolution of the input values is complete. The circuit as a whole enforces the completeness of input criteria for data.

The completion of resolution of an input data set can be determined by simply monitoring the result values. When the result values transition from all NULL to a complete result data value set (all data at the output), then the resolution of a complete set of input data values is finished. The circuit indicates its own completion of resolution, autonomously and purely symbolically. No external expression or authority such as a clock, delay line or controller is needed.