Abstract

A two-pass spatial transform technique that does not exhibit the aliasing artifacts associated with techniques for spatial transform of discrete sampled images is possible through the use of a complete and continuous resampling interpolation algorithm. The algorithm is complete in the sense that all the pixels of the input image under the map of the output image fully contribute to the output image. It is continuous in the sense that no gaps or overlaps exist in the sampling of the input pixels and that the sampling can be performed with arbitrary precision. The technique is real time in the sense that it can be guaranteed to operate for any arbitrary transform within a given time limit. Because of the complete and continuous nature of the resampling algorithm, the resulting image is free of the classic sampling artifacts such as graininess, degradation, and edge aliasing.

The advantage of a two-pass spatial transform technique over a one-pass technique has been that it offers a more effective and efficient match with current implementation technology. But only part of this advantage has been recognized. Previous thinking has focused on the mathematical notion of point, or coordinate, transforms mapping points of the output image to points in the input image. Resampling and interpolating input intensities about the mapped point to generate the output pixel intensity is a secondary concern. Distinct advantages can be gained simply by reversing this order of significance, that is, by considering first the intensity interpolation technique and second the way to impose spatial significance on the interpolation technique.

The overlooked advantage of the two-pass technique is that complete, continuous, and time-constrained intensity interpolation can be conveniently achieved in one dimension. I will present the basic one-dimensional interpolation algorithm and then show how two-dimensional spatial significance can be imposed on the interpolation algorithm to achieve a two-dimensional transform mapping.

The technique was developed intuitively and experimentally and will be presented in an intuitive style. The formal mathematical characterization has proved difficult. However, hardware has been built that performs two-dimensional image transforms in real time.

One-Dimensional Resampling Interpolation

The one-dimensional resampling interpolation algorithm maps a limited line of discrete input pixel intensity values into a limited line of discrete output pixel intensity values. The mapping is determined by a sizing factor of the output line in relation to the input line and by a position factor in relation to the output line. It can be characterized by the following formulation, where S is a scaling factor, a size factor of the output data in relation to the input data, and I/S is the inverse of the size factor. Note that S can vary pixel by pixel.

Each consecutive output pixel = S (1/S consecutive input pixels).

The inverse size factor indicates how much of an input pixel contributes to each successive output pixel, or OUTVAL. The size factor can be a constant for an entire line of pixels, or it can change for each new output pixel. The interpolation algorithm is illustrated in Figure 1.

Figure 1. Resampling interpolation algorithm.

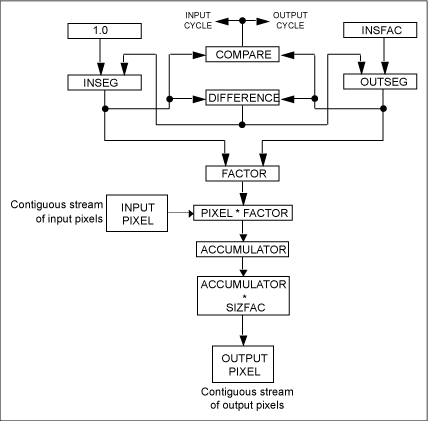
INSFAC is 1/S, or the inverse size factor; it indicates how much of an input pixel contributes to each output pixel.

SIZFAC the size factor, Is a direct multiplicative scale factor from input to output.

INSEG indicates how much of the current input pixel is available to contribute to the next output pixel.

OUTSEG indicates how much of an input pixel is required to complete the next output pixel.

Pixel is the intensity value of the current input pixel.

INSEG and OUTSEG can be viewed as fractional-valued pointers, or position markers, in the stream of contiguous input pixels.