Nonconstant-Size-Factor Mapping

So far only situations that perform an entire mapping with a constant size factor have been discussed. If the size factor, and hence INSFAC, are varied for each new output pixel, any arbitrary mapping of contiguous pixel values can be achieved.

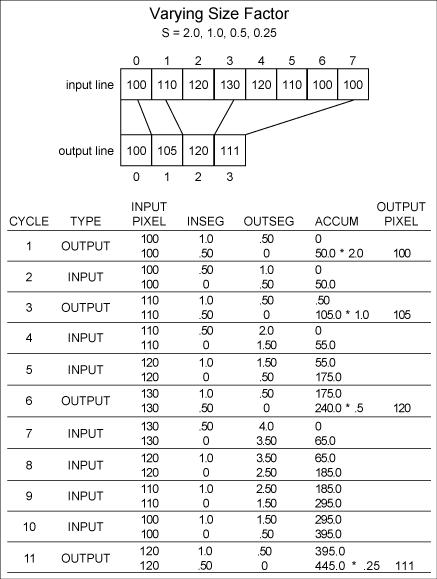
Figure 10 is a one-dimensional example of a mapping with a size factor that halves for each output pixel.

Figure 10. Example with varying size factor.

Limited-Time Performance

For contiguous mappings of consecutive input pixels into consecutive output pixels, a maximum time limit can be established. The nature of the interpolation algorithm is such that every cycle is either completing an output pixel or using up an input pixel. This includes zero cycles (see Figure 4). If there are 512 input pixels and a range of 512 possible output pixels, and if pretransform clipping is performed to ensure that only output pixels that fall within the output line are generated by the algorithm, then the algorithm will not use up more than 512 input pixels nor generate more than 512 output pixels. Any arbitrary contiguous mapping can be guaranteed to occur in 1024 cycles. A worst case, interestingly enough, is a size factor of 1.0 where, for instance, 512 output pixels are generated directly from the corresponding input pixel and 512 zero cycles are generated to get the next input pixel. A size factor of slightly less than 1.0 uses 1024 cycles with no zero cycles. This ability to deterministically bound the computation, plus the simplicity of the computation, makes the algorithm ideal for real-time implementation.

A Two-Dimensional Transform

Two-dimensional images can be spatially transformed by combining a series of one-dimensional interpolations in two passes over the image. The first pass, which we will consider to be the vertical pass, maps all input pixels into their correct vertical orientation and creates an intermediate image. The second, or horizontal, pass maps all the pixels from the intermediate image into their correct horizontal orientation to create the final output image. A technique of mapping to four target corner points to achieve size, translation, and rotation of an image can be used.

Four-Corner-to-Four-Corner Mapping Procedure

This procedure operates on an input image residing in a bounded image plane and maps the input image into a bounded output image plane. Line and column extents XBEG, XEND, YBEG, and YEND specify the bounds and the four corner points of the input image to be mapped. Four target corner points specify the corner points of the mapping in the output image plane. These target corner points can be computed by applying standard coordinate transforms to the input corner points.

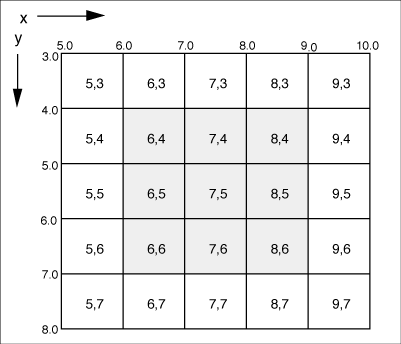
Both input and output images use a fractional-valued coordinate system overlaying the discrete grid of pixels, as shown in Figure 11. All computations are in relation to this reference system. The origin is at the upper-left corner, X values increase to the right and Y values increase downward.

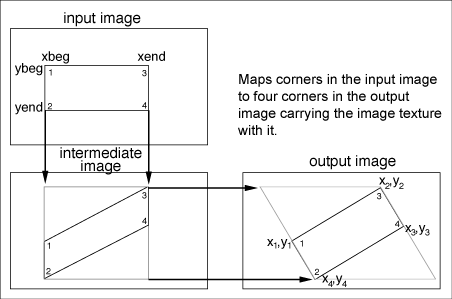
Figure 12 illustrates the four-corner transform. The input image corner points are labeled 1, 2, 3, 4, and the target corner points corresponding to the input points are similarly labeled. The figure shows the mapping from the input image to the intermediate image and the intermediate image to the output image.

The first, or vertical, pass maps all intensities into their correct vertical orientation column by column. Corner I must be mapped to Y1, and corner 4 must be mapped to Y4; therefore, the correct vertical orientation for the first, or leftmost, column of the input image is between Y1 and Y4. The correct vertical orientation for the last, or rightmost, column is between Y2 and Y3. The correct vertical orientation for all intervening columns is along uniformly interpolated positions between the first and last column.

Figure 11. Real-valued coordinate system over image.

Figure 12. Four-corner-to-four-corner mapping technique.

The real output location (ROTLOC) and size factor (SIZFAC) for the first column are:

ROTLOC = Y1

SIZFAC = ( Y4-Y1)/( YEND-YBEG + I)

The size factor for a rectangular output transform is a constant for all columns, but the output location varies. This variation is linear and can be accommodated by adding an increment (LOCDLT) to ROTLOC for each successive column. This increment is:

LOCDLT = ( Y2- Y1)/(XEND-XBEG)

The value of ROTLOC will be incremented by LOCDLT for each successive column one less time than the number of columns, and the output location (ROTLOC) for the last column will equal Y2. For nonrectangular output mappings, an increment can be similarly applied to the size factor.

The values to initialize the interpolation algorithm for each column are:

SIZFAC = SIZFAC

INSFAC = I/SIZFAC

INSEG = 1.0

OUTSEG = INSFAC * (1.0 - fraction (ROTLOC) )

OUTLOC = Integer (ROTLOC)

INLOC = YBEG

If ROTLOC is less than 0.0, clipping must be performed by projecting the left edge of the zero output pixel into the input line. The input line offset (INOFF) is:

INOFF = -ROTLOC * INSFAC

The values to initialize the interpolation algorithm for clipped columns are:

SIZFAC = SIZFAC

INSFAC = 1.0 /SIZFAC

INSEG = 1.0 - fraction (INOFF)

OUTSEG = INSFAC

OUTLOC = 1

INLOC = YBEG + Integer (INOFF)

After the interpolation process has operated on each column of the input image, an intermediate image is produced, as shown in Figure 12. The next step is to transform the intermediate image row by row into the output image.

The extents of the intermediate image are from XBEG to XEND and from Integer (Y2) to Integer (Y4). This bounding rectangle is the input to the second pass. The triangular areas in the rectangle outside the intermediate image must be set to zero.

The second pass basically maps the 4-1 edge of the inter- mediate image into the 4-1 edge projected through Y2 of the output image with a size factor such that the 2-3 edge of the intermediate image maps to the 2-3 edge of the output image.

Beginning at the top, the output location for the first row is the intersection of the 1-4 edge with Y = Y2.

ROTLOC = ((( Y2 - Y4) * (X1 - X4)) / ( Y1 - Y4)) + X4

The intermediate image line must be stretched a little to fit between ROTLOC and X2. The size factor is:

SIZFAC = (X2-ROTLOC) / (XEND - XBEG + 1)

The last ROTLOC must equal X4 after Integer ( Y4) - Integer ( Y2) increments, so the location delta is:

LOCDLT = (X4 - ROTLOC) / (Integer ( Y4) - Integer ( Y2))

The values to initialize the interpolation process for each row are:

SIZFAC = SIZFAC

INSFAC = 1/ SIZFAC

INSEG = 1.0

OUTSEG = INSFAC * (1.0 - fraction (ROTLOC) )

OUTLOC = Integer (ROTLOC)

INLOC = YBEG

These are identical to the values for the first pass. Clipping is also performed exactly as in the first pass.

Mapping of the first row, which consists mostly of zeros, begins at the initial ROTLOC with the proper size factor such that the data at corner 2 of the intermediate image maps into corner 2 of the output image. As for each successive row, ROTLOC moves along the 4-1 edge of the output image the 2-3 edge of the intermediate image is mapped to the 2-3 edge of the output image. The internal data of the image follows with these edge mappings through both passes and is itself correctly and proportionally mapped.