Figure 3. Example of expansion.

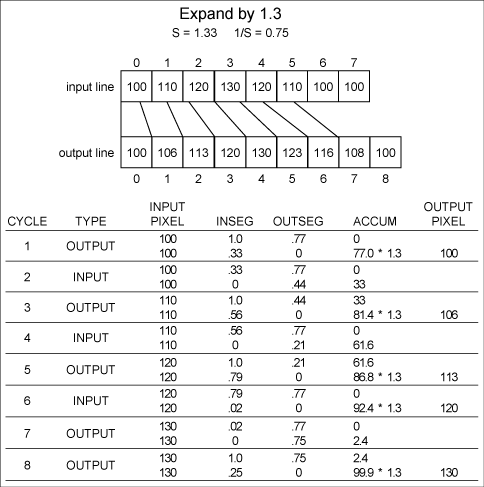
For the first cycle INSEG is smaller than OUTSEG. The input pixel intensity is multiplied by INSEG and added to the accumulator. INSEG is subtracted from OUTSEG, the next input pixel is addressed, and INSEG is reinitialized to 1.0.

For the second cycle OUTSEG is smaller. The input pixel is multiplied by OUTSEG and added to the accumulator. OUTSEG is subtracted from INSEG and is then reinitialized to 1.33. The contents of the accumulator are scaled by SIZFAC, producing the current output pixel value 102. The accumulator is zeroed, and the next output pixel is addressed.

For the third cycle INSEG is smaller. The input pixel intensity is multiplied by INSEG and added to the accumulator. INSEG is subtracted from OUTSEG, the next input pixel is addressed, and INSEG is reinitialized to 1.0.

For the fourth cycle OUTSEG is smaller. The input pixel is multiplied by OUTSEG and added to the accumulator. OUTSEG is subtracted from INSEG and is then reinitialized to 1.33. The contents of the accumulator are scaled by SIZFAC, producing the current output pixel value 115. The accumulator is zeroed, and the next output pixel is addressed.

This process continues until all input pixels are used up or until all output pixels are completed. Figure 3 is an example of an expanding size factor; Figure 4 is an example with zero cycles.

Figure 4. Example with 2 zero cycles.

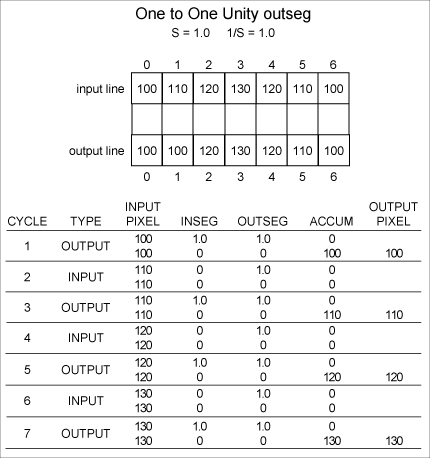
The transform is complete in that all the information from the input pixels contributed to the output pixels. The resampling of the line of input pixels is contiguous, without gaps, and without overlaps. The transform is continuous in that the interplay between INSEG and OUTSEG and the scaling of input pixels can be performed with arbitrary precision.

Precision Issues

The precision sensitivity of the interpolation algorithm is in the spatial domain rather than in the intensity domain. The algorithm will always produce a smooth output line free of intensity aliasing artifacts, but there may be spatial position inaccuracies in the output line. These inaccuracies can result in spatial jitter between consecutive spatial transforms on the right edge of the output line (assuming that the algorithm proceeds from left to right). This arises from the continued mutual subtraction of INSEG and OUTSEG. Notice in Figure 3 that the final value of INSEG is 0.01 when it should properly be 0.0. This is due to truncation from carrying only two decimal digits of precision. The significance of this 0.01 is that the output line will be slightly longer than it should be. After several hundred input pixels have been traversed, this error grows, and the last output pixel may be misplaced by one or more whole pixels beyond where it should properly be. Such a spatial misregistration is not important for many applications, but if it is important to the application, sufficient fractional precision must be carried with SIZFAC, INSFAC, INSEG, and OUTSEG to satisfy the application. For instance, to achieve 1/256 of a pixel accuracy over 512 input pixels, about 24 fraction bits are required.

The algorithm is very insensitive to pixel intensity mapping. The effects of precision on intensity mapping can only be seen at the extremes of shrinking and expanding, where factors overflow or underflow their precision range, suddenly go to zero, and the image disappears.

If, for instance, INSFAC has eight integer bits, it can specify that 255 input pixels be added to the accumulator, which will then be scaled by a SIZFAC of 1/255 to shrink a line by 1/255. A correct average of 255 input pixel intensities is generated for the output pixel. If, however, a SIZFAC of 1/256 is attempted, INSFAC must represent 256 and set a ninth integer bit, which it doesn't have, and it is suddenly zero. OUTSEG is always smaller and equal to zero, so that all output pixels are zero, and the output line disappears. There was not a gradual degradation, but there was integrity of intensity mapping until the limit of precision was reached.

The same thing occurs during expansion, where SIZFAC is large. The intensity mapping is quite correct until INSFAC underflows its fraction bits, becomes zero, and the output line again disappears.

Subpixel Positioning

Output lines can be subpixel positioned, or phased in the output line, by scaling the output pixel intensity value proportionally to the fractional part of the output pixel to be represented. A fractional value scale can be superimposed on the pixel number scale as shown in Figure 5. The fractional position value 1.5 is halfway through pixel 1. To position a line beginning at 1.5, the first output pixel should be half its normal intensity value. This can be accomplished simply by initializing OUTSEG to 0.5 of INSFAC instead of 1.0 of INSFAC. This makes the first, or leftmost, pixel of the output line a partial-intensity pixel and shifts the mapping of the entire line by half an output pixel.

Figure 5. Real-valued scale over pixel grid.

When the algorithm runs out of input pixels, the value left in the accumulator is very likely not a full output pixel's worth. This value is scaled by SIZFAC and output as the last output pixel, which will also be a partial-intensity pixel. So partial-intensity output pixels are generated at the beginning and end of the output line to represent continuous subpixel positioning of the output line.

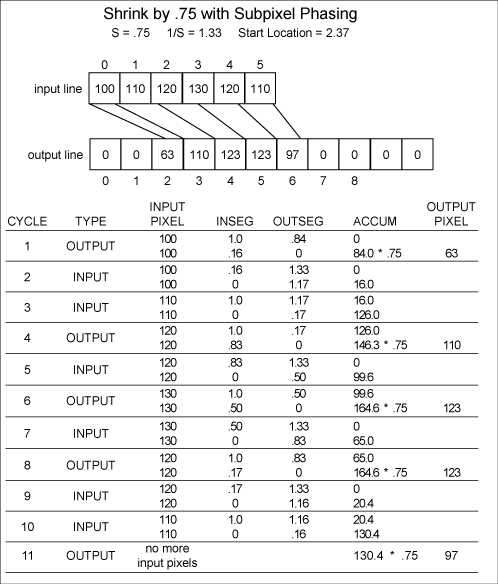
The example in Figure 6 positions an output line with a size factor of 0.75 to begin at output location 2.37. The first output pixel location is set to 2, and the initial value of OUTSEG is (1.0-0.63) * INSFAC to indicate 0.63 of full intensity for the first output pixel. Notice the partial intensity for the last output pixel.

Figure 6. Example of subpixel phasing.