Output Clipping

Clipping is the process of ignoring output pixels that don't fall within the output line. These pixels can be ignored prior to being calculated.

By projecting the left edge of the output line into the input pixel line, it can be determined where in the input pixel line the first output pixel should begin. This point is unlikely to be on an input pixel boundary, which means that interpolation should begin with a partial input pixel. This can be simply accommodated by initializing the first value of INSEG to a value less than 1.0. In this manner all beginning border pixels in the output line can be properly mapped.

FIGURE 7. Example of clipping.

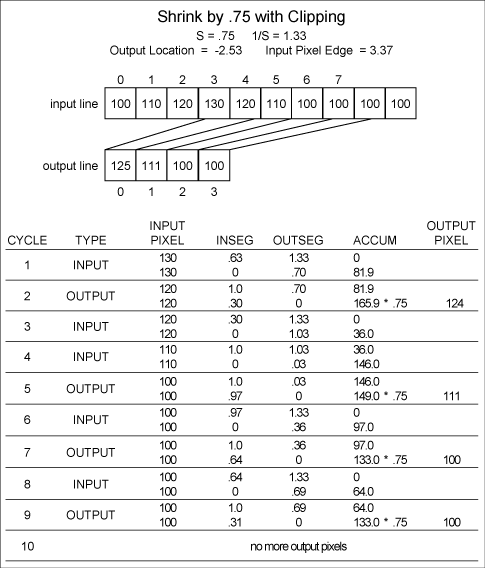
Figure 7 illustrates clipping where the output line is to begin at -2.53 with a size factor of 0.75. If the beginning of the first input pixel maps to -2.53 in the output line, then we have to move 2.53 output pixels' worth of input pixels into the input line. This input offset (INOFF) is:

INOFF = 2.53 * 1.33 = 3.37

To begin at input pixel location 3.37, just set the input pixel to 3 and INSEG to:

INSEG = 1.0-0.37 = 0.63

End-of-line clipping is automatically accommodated by simply terminating when the last whole output pixel is generated. The last output pixel at the end of the line will automatically be a properly mapped output pixel.

Expansion Smoothing

Expansion with the algorithm as described results in a blocky output image. As illustrated in Figure 8, several output pixels of identical value are generated from a single pixel. These areas of identical value lend a blockiness to the output line. This can be accommodated with a simple expedient. Instead of inputting raw pixel values to the interpolation algorithm, we can take pixel values from a one-pixel-wide averaging window traversing the raw input pixels based on the value of INSEG. INSEG can be viewed as a pointer to the spatial position of utilization of input pixels. The averaging window can be viewed as delivering one pixel's worth of input value beginning at INSEG.

Figure 8. Example of expansion blockiness.

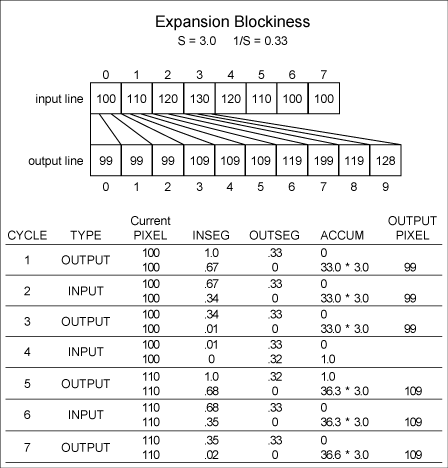
This relationship is:

input pixel = INSEG * current pixel + (1.0- INSEG) * next pixel

The operation of the averaging window and its effect on the output is illustrated in Figure 9.

During shrinking the averaging window is ineffective because INSEG is 1.0 most of the time, effectively disabling the averaging. Therefore the window can be operated continuously for all transforms, whether they are expanding or shrinking.

Figure 9. Example of expansion with averaging window.
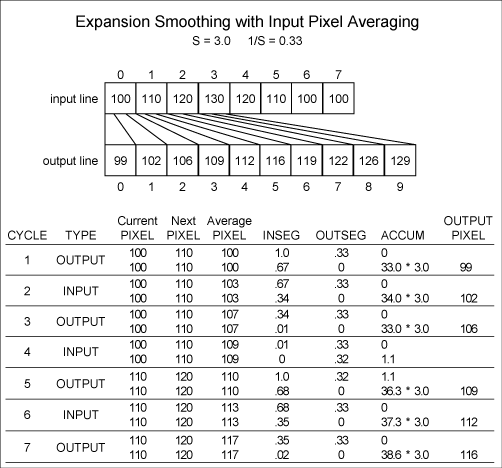