2NCL Expression Unit Functions

2NCL gates can be composed into expressions that are not logically determined in any sense at any boundary. So there must be rules of effective design associated with 2NCL. Basically a 2NCL expression unit must enforce the completeness criterion between a variable level input boundary and variable level output boundary and must limit orphan signal paths. These rules can be isolated from the system designer by providing a library of 2NCL expression units that are correctly formed and fully logically determined at their variable level boundaries. The designer can then freely compose these expression units into combinational expressions that are fully logically determined as a whole in exactly the same sense that 4NCL and 3NCL gates inherently compose into combinational expressions that are fully logically determined as a whole. The first order demonstration of this is the set of expression units of Figure 15 which is sufficient to map any Boolean combinational expression into a logically determined 2NCL combinational expression.

The Fate of Logical Determinability

3NCL is less logically expressive than 4NCL and 2NCL is less logically expressive than 3NCL. To form a complete expression of combinational behavior, the loss of logical expressivity had to be compensated with expression about timing relationships among signals. 4NCL gates are purely combinational gates and are fully logically determined. 3NCL gates are logically determined at the gate boundaries and any logical ambiguity (the feedback path) is isolated inside the gate. With 2NCL, there is a multi gate unit of expression between logically determined boundaries. 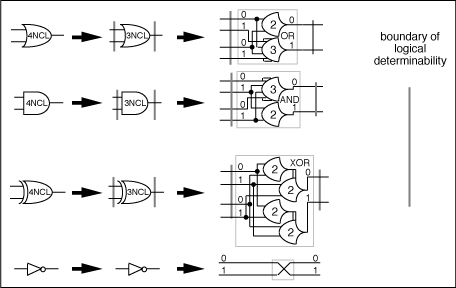This expression unit contains logical ambiguities (orphans) which are isolated between its logically determined boundaries. Figure 20 shows the boundaries of logical determinability as logical expressivity is compromised with successively less expressive logic families.

Figure 20. Logically determined boundary relationships between NULL Convention Logics.

Further Compromising Logical Completeness

A path has been followed of inescapable loss of logical completeness because of the inadequacies of successively less expressive logics. One can also choose to erode logical completeness for practical reasons. To the extent that one can make reliable assumptions about expression behavior one does not need to logically express that behavior. Of course, all the assumptions must then be made true in any actual implementation.

While for 4NCL and 3NCL the logical determinability of any combination of gates is inherent, this is not the case for 2NCL. A 2NCL expression must be properly formed to express the correct completeness relationships. Less logically determined 2NCL expressions can be composed erroneously but they can also be composed deliberately as an engineering trade-off decision.

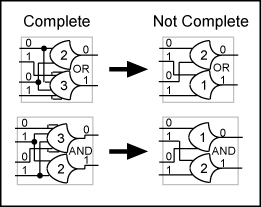
One can choose, for instance, to move the logically determined completeness boundaries even farther apart. The 2NCL AND and OR functions can be expressed with simpler gates that do not express the completeness criterion. The right-hand expressions of Figure 21 expresses the same data transformation function as the left-hand expressions of Figure 21 but they can generate an output without having a complete input data set. The boundaries of the expressions do not express the completeness criterion are not logically determined.

Figure 21. 2NCL AND and OR functions that do not enforce the completeness criterion.

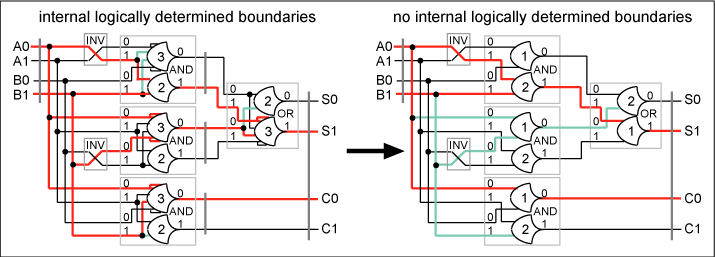
If these gates are substituted in the expression in the left-hand side of Figure 22 the result is the right-hand expression of Figure 22 which contains simpler logical elements. This circuit preserves the completeness criterion for the circuit as a whole but the completeness boundaries are farther apart and the orphan paths are longer requiring more precise assumptions about delay relationships. The reduced logical expressivity necessitates more expression of temporal relationships to completely express the process behavior.

Figure 22. 2NCL Half-adder with no internal logically determined completeness boundaries.

No Logically Determined Boundaries at All

One might wish to compromise the logical completeness of expression to the point where there are no logically determined boundaries at all in the data path combinational expressions. If there are no logically determined completeness boundaries and the completeness criterion is not in play, there is little point in using NULL Convention Logic for the combinational expressions. It would be more efficient to use the less expressive Boolean logic.

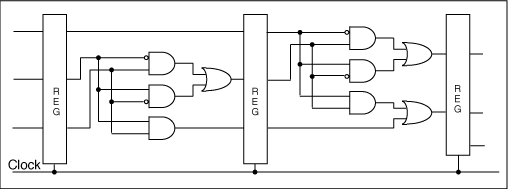
If the combinational expressions are not logically determinable then they must be determined by timing relationships. One can assume that all combinational expressions complete their resolution with a given time period. A single global signal distributed to each combinational expression expressing the single time period will suffice. The result is clocked Boolean logic shown in Figure 23. One must then insure that all combinational expressions do indeed complete within the allotted period and that the clock signal is reliably distributed to all registers.

This is the form of least logical determinability and of the most temporal expression. There are no logically determined completeness boundaries anywhere in the system.

Figure 23. Clocked Boolean logic.