The
Time Relationship
The
feedback path R must stabilize strictly before
the next wavefront is presented to the gate. The
presentation of the next wavefront will not occur
until the current wavefront has flowed through
the combinational expression and through the watcher,
the acknowledge signal has flowed to the regulator
and the regulator has allowed the next wavefront
to flow into the combinational expression. This
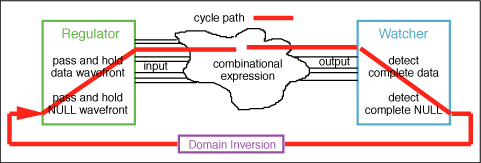
will be referred to as the NCL cycle path shown
in Figure 9. The cycle path
propagation time for a particular expression is
the cycle period of the expression. If the feedback
signal path of a gate is slower than the cycle
period of the expression, there is a critical
hazard and the gate can behave incorrectly so
this temporal relationship must be considered
in the complete expression of behavior. However,
this feedback path can be isolated inside the
gate and its time relationship can be easily rendered
insignificant in relation to the cycle period
of the expression.
Figure
9. The NCL cycle path.
The
Compromise to Logical Completenesses
The
completeness criterion and completeness of participation
are still intact but single-form completeness
of expression has been compromised. The behavior
of the expression is no longer characterized completely
in terms of logical relationships. An expression
of time must also be included to completely express
the behavior of a combinational process. However,
it is clear where in the expression of single
form completeness has been compromised, it is
clear that this compromise can be benignly isolated
inside a gate and it is clear to what extent logical
completeness can still be considered with advantage.
Assuming effective isolation inside each gate,
the input and output boundaries of the gates still
form logically determined completeness boundaries
that compose to logically determined combinational
expressions just like 4NCL.
Relationship
of 3NCL to Boolean Logic
3NCL
still differentiates two data values and can be
mapped gate for gate to Boolean logic expressions.
Can
a 2 value logic be logically complete?
If
the expressivity of the logic is reduced to only
two values, it must be decided what those two
values will differentiate. 4NCL and 3NCL differentiate
data states from non-data states and also differentiate
two data states. If only two logic values are
available only one of these differentiations can
be expressed.
If
it is decided to differentiate two data values
with the logical values such as TRUE and FALSE
the resulting logic is Boolean logic. A Boolean
logic expression constantly expresses data and
cannot differentiate data from non-data. For a
Boolean logic combinational expression the differentiation
of successive data sets and the beginning and
ending of a data set resolution must be expressed
non-logically with some convention of time relationship
such as a clock or delay element.
If
it is decided to differentiate data from non-data,
the NULL convention can be continued with the
logical values DATA and NULL and the hysteresis
behavior can be retained. The resulting logic
is 2 value NULL Convention Logic (2NCL). In this
case the differentiation of data values is no
longer expressed logically and must be expressed
non-logically with a multiple signal path data
representation convention. Figure
10 shows the correspondences between all four
logics.
Figure
10. Correspondence of the logics.
| 4NCL |
3NCL |
2NCL |
Boolean
Logic |
| TRUE |
TRUE |
|
TRUE |
| FALSE |
FALSE |
DATA |
FALSE |
| INTERMEDIATE |
Hysteresis
Behavior |
Hysteresis
Behavior |
|
| NULL |
NULL |
NULL |
|
The
Data Representation Convention
Since,
in 2NCL, there is only one DATA value, each signal
path in a 2NCL expression represents one specific
meaning and the path either asserts its meaning
(DATA) or does not assert its meaning (NULL).
To represent a variable that can express multiple
mutually exclusive values multiple signal paths
must be used. To form a binary variable that mutually
exclusively expresses TRUE and FALSE, for instance,
there must be two signal paths, one signal path
meaning TRUE and one signal path meaning FALSE.
For any data wavefront only one of the two paths
may express its DATA value. It is illegal for
both DATA values to be simultaneously expressed.
The two signal paths then form a single dual-rail
variable that can express two mutually exclusive
DATA values or NULL as shown in Figure
11.
Figure
11. 2 value NCL variable formed from two signal
paths.

In
general, an N value NCL variable can be represented
with N signal paths only one of which will assert
a DATA value in a given data wavefront [reference
7]. Figure 12 shows several
examples of NCL multi-value variables.
Figure
12. Multi path NCL variables.
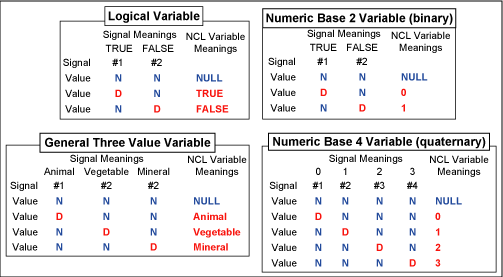
Each
signal path is a value of a variable. This is
in contrast to the familiar situation of each
signal path constituting a whole variable. Variables
of any size can be built from signal paths and
arbitrary mutually exclusive meanings can be assigned
to the paths. This property is useful for implementing
higher radix and even mixed radix numeric functions
and for control expressions. For instance, the
familiar one-hot control code, derived typically
from a decode, becomes a single large NCL variable.
In this sense, 2NCL is a general multi-value logic.
For
a data wavefront, each variable asserts exactly
one DATA value. Completeness of the data wavefront
is exactly one DATA value per variable. For a
NULL wavefront all asserted DATA values return
to NULL and completeness for a NULL wavefront
is all NULL values across all variables.
|