The 2NCL Orphan Path

While the behavior of variables at the boundaries of an expression unit are logically determined, there are individual signal paths inside the expression unit that are not logically determined. For each data wavefront through an expression unit there will be an effective transition path which is a logically determined irredundant path from the input through the expression unit that generates the output. When the output transitions to complete DATA it implies that the input data set is complete and that the transitions to DATA have propagated over the effective path to the output. There will also be ineffective paths branching off this effective path that do not contribute to the output and therefore are not logically determined by the output. 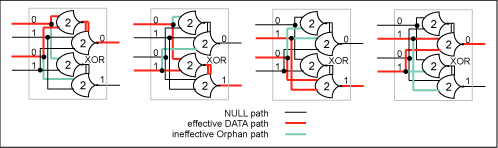These ineffective paths will be called orphans because they have lost all of their logical relations. Figure 16 shows the effective path and orphan paths for all four data configurations of the XOR expression unit.

Figure 16. Effective paths and orphan paths through the XOR gate equivalent expression.

A slow orphan path is not a problem for an individual data wavefront because the orphan paths do not contribute to the output nor can they confuse the generation of the output. The difficulty arises with the possibility of a slow orphan getting mixed up with a succeeding data wavefront.

Upon completion of the data wavefront at the output, the NULL wavefront will be requested and presented to the input of the expression while orphans may still be transitioning to DATA. The output of the expression transitioning to all NULL implies that the input and the entire effective path has transitioned to NULL but it does not imply that the orphans have transitioned to NULL. The next DATA wavefront is requested and if all the orphan paths from the previous data wavefront have not transitioned to NULL, the next data wavefront can interact with the slow orphan in a non logically determined way. Ambiguous resolution, hazards, glitches and chaos can ensue.

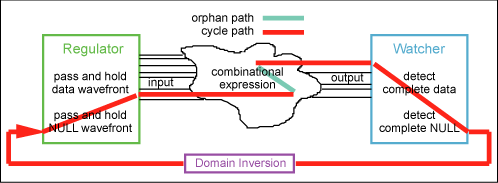
The succeeding wavefront will arrive in one cycle period of the expression. So the complete characterization of the behavior of a 2NCL expression must include the timing relationship that all orphan paths must completely transition strictly faster than the cycle period of the expression. Figure 17 shows an orphan path in relation to the full cycle path of an expression.

Figure 17. The orphan path in relation to the cycle path.

Logical Isolation of Orphans

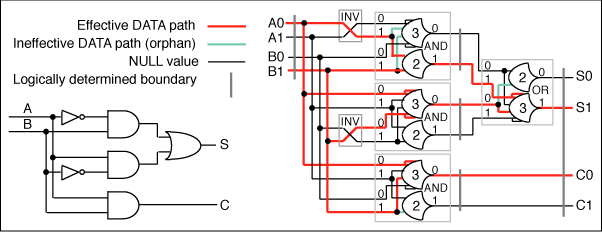
Orphan paths do not cross logically determined completeness boundaries. If they did, the boundaries would not be logically determined. Orphans are isolated between the logically determined completeness boundaries of expression units. Figure 18 provides an example of a 2NCL expression generated from a Boolean logic expression by direct gate substitution. Each gate equivalent expression unit was logically determined at its boundaries and those boundaries become internal to the greater combinational expression. The effective path for A = 0 and B = 1 is shown with the associated orphan paths. It can be seen that all orphan paths are isolated between the logically determined completeness boundaries of each expression unit.

Figure 18. 2NCL expression by direct gate substitution of a Boolean circuit.

It is possible for an orphan path to include gates and to be arbitrarily long but an orphan path can always be limited to a local signal path by making the portion of the orphan path which includes gates an output variable subject to completion determination. 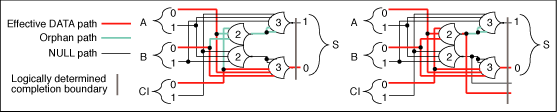The part of the path including the gate then becomes an effective data path that is logically determined by the output thus shortening the orphan path to a local signal path that does not include a gate. The left expression of Figure 19 shows a 2NCL expression with an orphan path that includes a gate. The right expression of Figure 19 shows a new logically determined boundary created by including part of the orphan path in the completion determination of the output.

Figure 19. Orphan path through gate limited to local path with a created output variable.

The orphan paths are the only logical ambiguity (delay sensitivity) associated with 2NCL and they can be limited to local signal paths isolated inside expression units and their delay behavior can be made insignificant in relation to the cycle time of the expression.