2NCL as a Threshold Logic

NULL means not-data, so the NULL value cannot be considered in resolving data value sets. Since each input to a gate expresses only one data value there can be no combinations of different data values as in Boolean logic, there can only be combinations of the single DATA value. The only discriminable property available when combining DATA values at the input to a gate is how many DATA values are presented. Therefore, 2NCL gates can be naturally viewed as a threshold logic comprising discrete M of N threshold gates with hysteresis behavior.

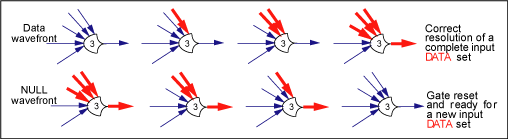
Figure 13 illustrates the graphical representation and the behavior of a 3 of 5 gate. The number inside the gate indicates the threshold of the gate M and the input connections indicate the N. Thin lines are NULL. Wide red lines are DATA. Beginning in a NULL state with all inputs NULL and asserting a NULL result value, the gate will not assert a DATA result value until its input data set is complete, which in this case is three data values. Then the gate will maintain the DATA value until all of its input values are NULL at which time it will transition to a NULL result value.

Figure 13. Hysteresis behavior of 2NCL gate.

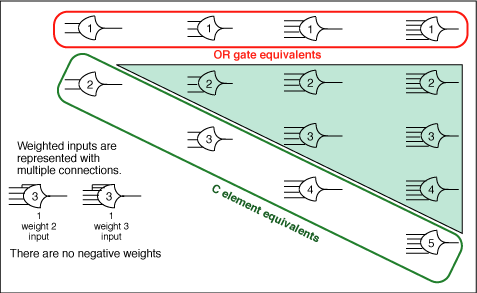
Figure 8 shows the 2NCL family of logic gates noting correspondences to familiar gate functions. Weighted inputs are shown as multiply connected inputs. There are no negatively weighted inputs. Each gate expresses the completeness criterion for both data in relation to NULL and for NULL in relation to data. Each gate and any combination of gates expresses the universal NULL function. Notice that there is no equivalent to the Boolean AND gate and there is no inverter.

Figure 14. 2NCL family of logic gates.

There is not as strong an intersection of 2NCL with classic threshold logic synthesis [references: 8, 9, 10] as might be expected because neither hysteresis behavior nor completeness relationships were considered.

2NCL in Relation to Boolean Logic

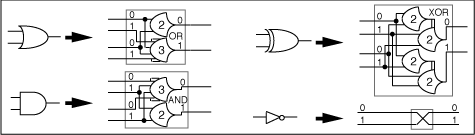
Figure 15 shows the 2NCL equivalents to the Boolean gate functions. Each gate equivalent has two dual-rail inputs and one dual-rail output. The inversion has one dual-rail input and one dual-rail output.

Figure 15. 2NCL mappings for Boolean functions.

Unateness, Monotonicity and Hazard Freeness

The first thing to note is that variable inversion does not involve signal path inversion. It is just a relabeling of the signal paths of the variable. Any single variable function including the complement function for any size variable is just a mapping of each input value to an output value and in the multi-path representation this can be expressed by simply relabeling the paths according to the mapping. There is no sense to inverting a signal path in a 2NCL combinational expression. All 2NCL combinational expressions are strictly unate at the signal level. During a DATA wavefront there are only transitions from NULL to DATA. There are no transitions from DATA to NULL. During a NULL wavefront there are only transitions from DATA to NULL. There are no transitions from NULL to DATA.

Sub-Variable Expressivity

The next thing to note is that the mapping is no longer gate for gate. The Boolean gate equivalent functions are multi 2NCL gate expressions. While Boolean gates are dealing with inputs and outputs that are whole variables, 2NCL gates are dealing with inputs and outputs that are individual values of variables. For instance the 2 of 2 gate in the OR expression of Figure 15 has as input the zero value path from each input variable but does not consider the 1 value path from either variable. In this sense 2NCL might be called a sub variable logic. One significant consequence of this is that completeness criterion and completeness of participation are lost at the signal path level and at the logic gate level.

Completeness at the Variable Level

While completeness criterion and completeness of participation have been lost at the signal path and gate level, these completenesses can be maintained at the variable level with units of expression that have whole variables as input and output. The 2NCL expressions of Figure 15 do not transition their output variables from NULL to DATA until the input variables are completely DATA (one DATA value per variable) and then do not transition their output variables to NULL until the input variables are completely NULL. The variable level boundaries of each expression unit are a logically determined completeness boundaries that express the completeness criterion at the variable level for the expression unit as a whole. These 2NCL expression units are functionally identical to 3NCL gates. They can be directly substituted for Boolean gates as in Figure 6 or can be otherwise composed to form 2NCL combinational expressions that, as a whole, expresses the completeness criterion and completeness of participation.